Computational Geometry | Generative Art
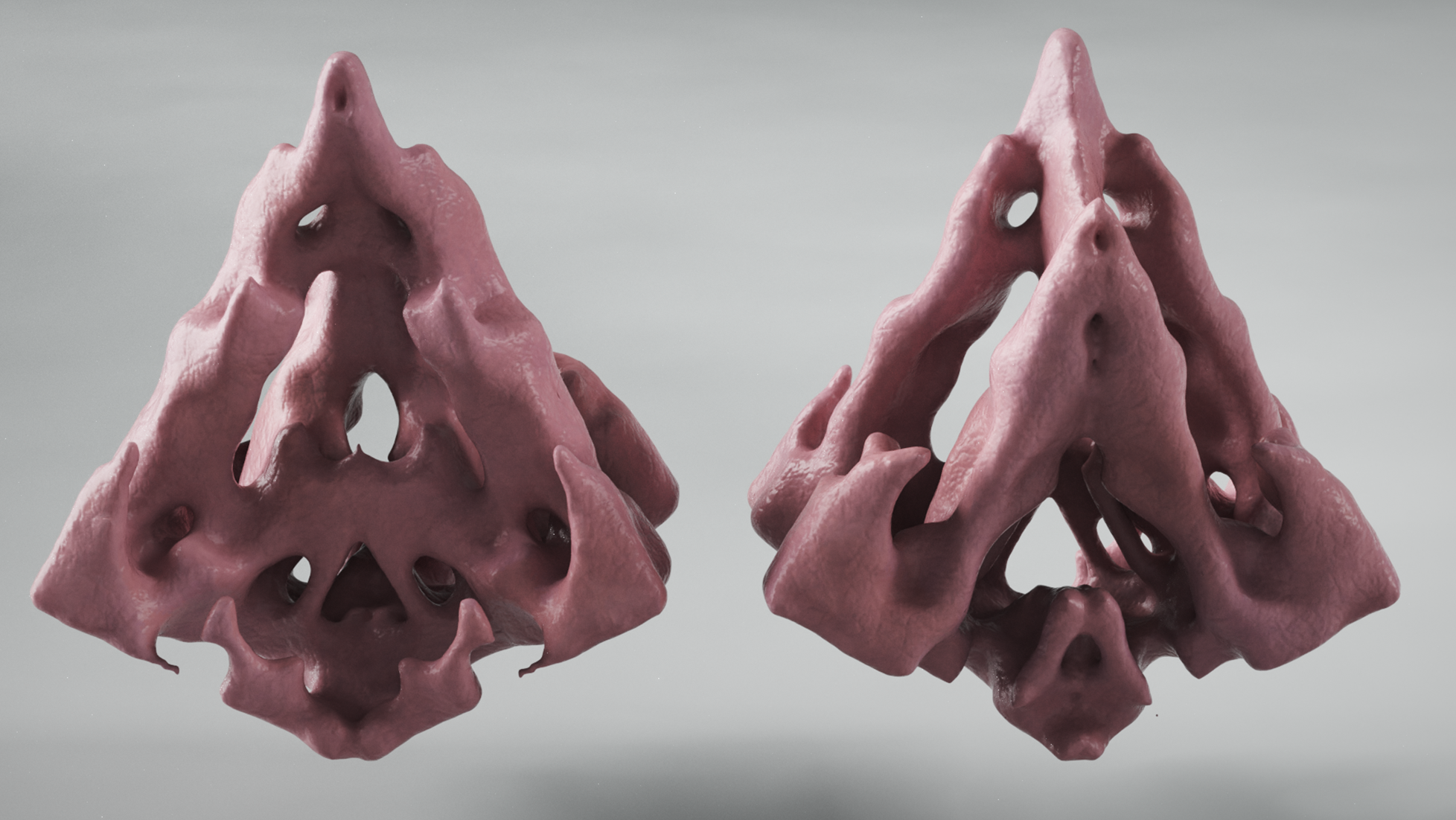
This project explores the use of cellular automata (CA) as a generative tool for form-finding in 3D spaces. Inspired by Conway's Game of Life, this investigation applies its fundamental rules to voxel grids to evolve complex, organic shapes. By utilizing a 3D CA system with rules for under-population, survival, over-population, and reproduction, dynamic forms emerge, evolving through iterative processes. This exploration aims to demonstrate how mathematical principles can inform creative design and generate both stable and evolving structures. The process, analysis, and results showcase the potential of CA in digital design workflows.











This project utilizes a 3D cellular automata system to explore the generative design of complex forms. The system is based on Conway’s Game of Life but extended into three dimensions, where each cell (voxel) has 26 potential neighbors. The system follows four fundamental rules:
Under-population: A live cell with fewer than two live neighbors dies.
Survival: A live cell with two or three live neighbors survives to the next generation.
Over-population: A live cell with more than three live neighbors dies.
Reproduction: A dead cell with exactly three live neighbors becomes alive.
In Grasshopper, the voxel grid is created using parameters for grid size, voxel resolution, and initial randomness. A random seed initializes the grid, with cells assigned a state of either alive or dead based on probability. The neighbor states are calculated using Euclidean distance, and each iteration applies the rules to evolve the grid’s state. This process is repeated across multiple generations to form complex, organic structures. The resulting forms are visualized through varying colors to represent alive and dead cells. Additionally, the system’s flexibility allows for the exploration of various parameters, such as grid size, neighbor radius, and mutation rates, which influence the final shapes